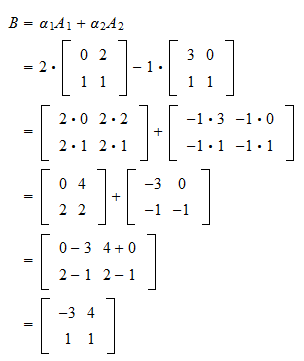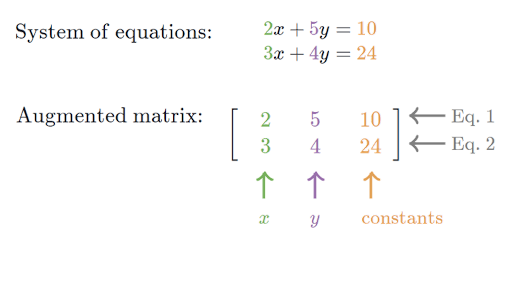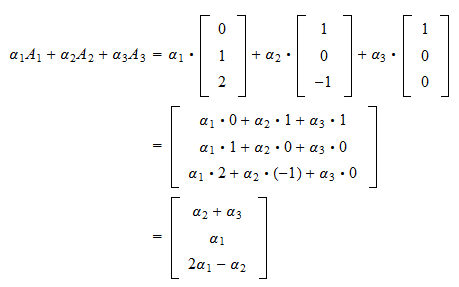Matrix Multiplication As Linear Combination Of Columns

11 Sep, 2021

The result is another column vector - a linear combination of xs columns with a b c as the. 2 4 1 2 4 5 3 7 3 5 x 1 x 2 2 4 2 5 7 3 5 The vector b is the same as the 2nd column of A so we can nd this solution by inspection the answer is x 0 1.

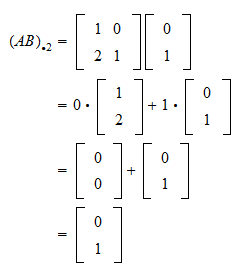
Matrix Multiplication And Linear Combinations

Cn 1 C Ais an n-by-1 matrix.

Matrix multiplication as linear combination of columns. Answered Oct 21 13 at 1941. Matrix Times a Column Vector Linear combination of columns Suppose A is an m-by-n matrix and c 0 B c1. The implication for the matrix productABis that each of its columnsABj is alinear combination of the columns ofA with coe.

So the third column of matrix A B is given by. We call Axa product and use multiplicative notation forreasons that will become clear shortly. In other words Ac is a linear combination of the columns of A with the scalars that multiply the columns coming from c.

If we multiply anmnmatrix by a vector inRn the result is. Provided that they have the same dimensions each matrix has the same number of rows and the same number of columns as. OfA with the scalars multiplying these columns taken in order from top to bottomfromv.

Ac 1 0 0 1 1 0 0 1 1 c1 c2 c3 c1 c2 c1 c3 c2 b1 b2 b3 b. A matrix is a linear combination of if and only if there exist scalars called coefficients of the linear combination such that In other words if you take a set of matrices you multiply each of them by a scalar and you add together all the products thus obtained then you obtain a linear combination. We can only multiply anmnmatrix by a vector inRnThat is inAxthe matrix must have as many columns as thevector has entries.

3 4 2 3 7 5 6 4 5 3 4 5 0 4 4 3 9 5 So the third column represented as a linear combination of columns of A is given by. Multiply this vector by the scalar a. For example the dimension of the matrix below is 2 3 read two by three because there are two rows and three columns.

Edited Oct 21 13 at 1952. 2 4 1 2 4 5 3 7 3 5 x 1 x 2 2 4 b 1 b 2 b 3 3 5 is a system with 3 equations and 2 unknowns. Given n n vectors u1u2u3un u 1 u 2 u 3 u n from Cm C m and n n scalars α1 α2α3αn α 1 α 2 α 3 α n their linear combination is the vector α1u1α2u2 α3u3αnun α 1 u 1 α 2 u 2 α 3 u 3 α n u n.

Sticking the white box with a in it to a vector just means. Now if we use all our vectors as columns of a matrix A that matrix multiplies the vector c c1 c2 c3. When multiplying two matrices theres a manual procedure we all know how to go through.

As one example of this the oft-used Theorem SLSLC said that every solution to a system of linear equations gives rise to a linear combination of the column vectors of the coefficient matrix that equals the vector of constants. Each result cell is computed separately as the dot-product of a row in the first matrix with a column in the second matrix. So this definition takes an equal number of scalars and vectors combines them using our two new operations scalar multiplication and vector addition and creates a single brand-new.

Definition MVP Matrix-Vector Product. Then Ac c1A1 cnAn. In fact there are three different dimensions involved in matrix multiplication when you multiply an M x L matrix A with an L x N matrix B to get an M x N matrix C.

Simply5a linear combination of the columns v1A1v2A2 vnAn. This theorem and others motivate the following central definition. Linear combination of columns of A gives the vector b.

This gives a new view-point to look at it. Second you use the two dimensions rows and columns which are the dimensions of the resulting matrix which is confusing because the number of columns in A is rows. Now instead of being just numbers c1 c2 c3 are now also forming a vector.

While its the easiest way to compute the result manually it may obscure a very interesting property of the. For example For each given matrix and vector determine whether is a linear combination of the columns of. We introduce matrix-vector and matrix-matrix multiplication and interpret matrix-vector multiplication as linear combination of the columns of the matrix.

In mathematics a matrix plural matrices is a rectangular array or table of numbers symbols or expressions arranged in rows and columns. 4 3 6 0 3 2 5 4 5 7 4 9 Share. But notice that this more general linear equation from Example 2.

Visualizing matrix multiplication as a linear combination. 8 4 5 1 9 7 0 3 1 2 1 A 3 8 1 1 4 9 2 5 7 30 8. If possible express as a linear combination of the columns of.

Recall that the product of a matrix and a vector can be interpreted as a linear combination of the columns of the matrix.

Pin On Math

Linear Combinations

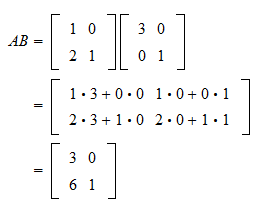
Matrix Multiplication And Linear Combinations

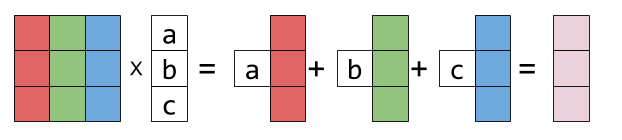
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data

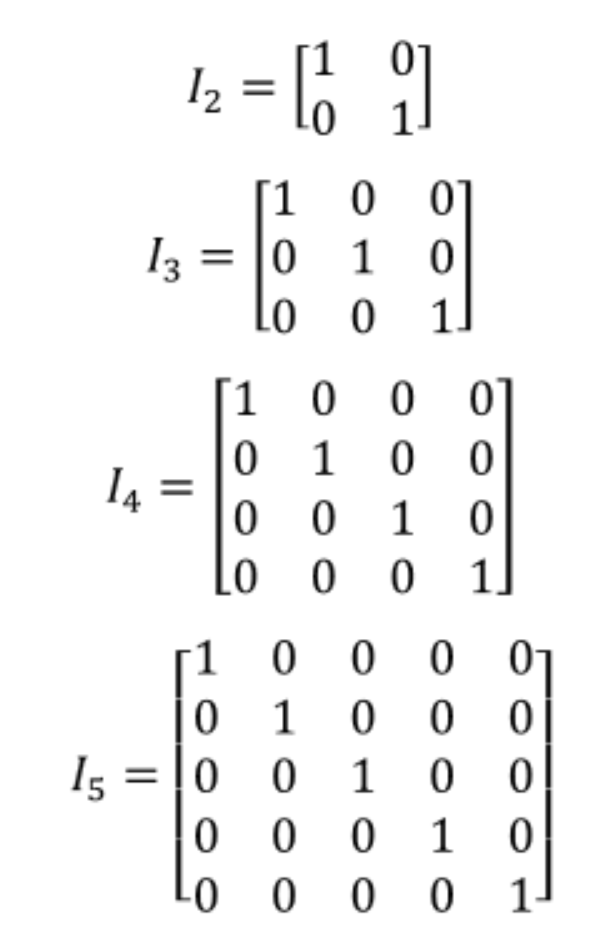
What Is An Identity Matrix Studypug

Ltr 0080 Matrix Of A Linear Transformation With Respect To Arbitrary Bases Ximera

Pin On Matrices

Pin On Scitech

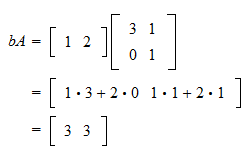
Matrix Multiplication And Linear Combinations

An Intuitive Guide To Linear Algebra Algebra Matrix Multiplication Linear

Nonsquare Matrices As Transformations Between Dimensions Essence Of Li Algebra Matrix Multiplication Matrix

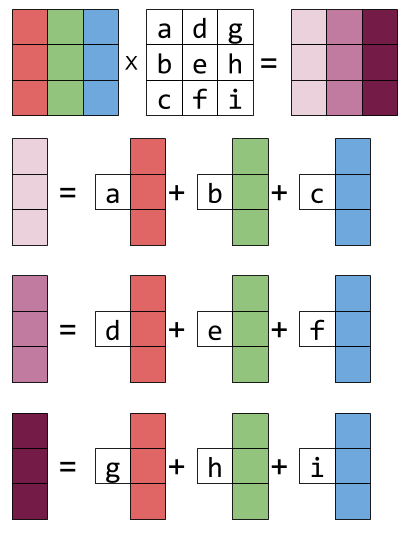
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data

Linear Algebra Example Problems The Matrix Product Ax Youtube

The Determinant Essence Of Linear Algebra Chapter 6 Youtube Algebra Basic Math Essence

Matrix Element Row Column Order Of Matrix Determinant Types Of Matrices Ad Joint Transpose Of Matrix Cbse Math 12th Product Of Matrix Math Multiplication

Representing Linear Systems With Matrices Article Khan Academy

Linear Combinations

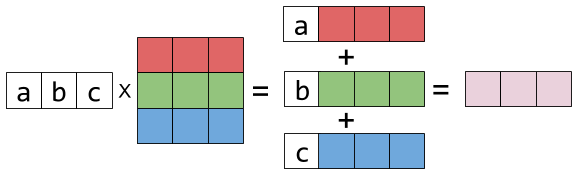
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data